Forced oscillations of systems with one degree of freedom
without taking into account resistance forces. Phenomenon of resonance
We will also consider this type of oscillations using the beam shown in Fig. 7 as an example.
We will assume a dynamic load in the form of a harmonic load changing according to a
sinusoidal law, i.e. P(t)=Psinθt, where P and θ are, respectively, the maximum component
(amplitude) of the load and the circular frequency of the disturbing force. Assuming that the
direction of displacement of the mass m coincides with the direction of action of the force
P(t), we will make the equation of dynamic equilibrium
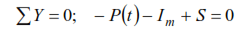
or 
Dividing the terms of the last equality by m and denoting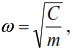 
we obtain a nonhomogeneous
differential equation in the form
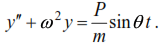
The solution of equation (13) in steady state has the form:
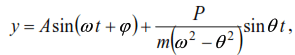
From equality (14) it follows that forced oscillations occur with the same frequency as the
disturbing force, and the amplitude of driven oscillations ydyn depends on the value of the
component P of the disturbing force P(t) and the ratio of the frequencies of free and driven
oscillations.
