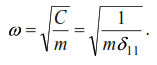If in the first condition at t=0 we take y=0, then C2=y0=0 and the oscillation equation (4) takes the form:
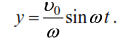
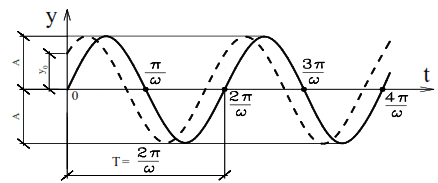
Equation (6) is a function of time, the graph of which is shown in Fig.6. The oscillations are performed according to a sinusoidal law. In Fig.6, the dashed line shows the graph of the equality function (4), from which it follows that for values t=0, t=π/ω, t=2π/ω, etc., the mass will not be on the equilibrium line, but will be shifted by the value y0.
The time it takes for the mass to complete one complete cycle of oscillations is called the period of oscillations. According to Fig. 6
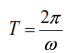
The number of complete oscillation cycles per unit time is called the oscillation frequency. From equality (7) we have:
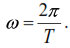
The frequency of oscillations per second is expressed in Hertz and is equal to:
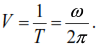
In practical calculations, the so-called technical frequency is often used, expressing the number of complete oscillation cycles in one minute.According to formula (8), we have:
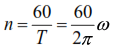
Above (2) is denoted by where C is the force providing a displacement equal to one. In relation to the total yst caused by the force P , the value of C is expressed by the equality:
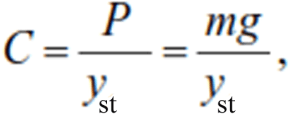
Substituting the last expression into formula (2), we have:
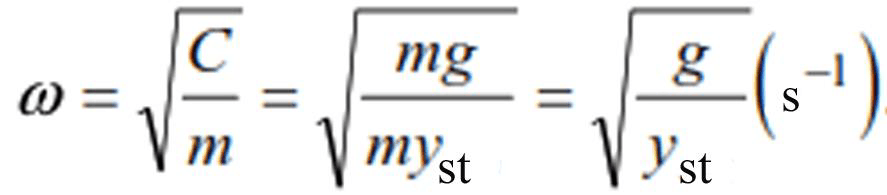
As is known g = 981 cm/sec2.Taking g≈(10π)2 and substituting expression (10) into the
technical frequency formula (9), we obtain:
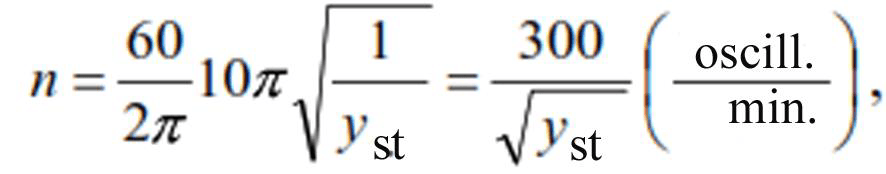
where yst should be taken in centimeters.
Formula (2) can be transformed into another form. From the definition of rigidity C of the
system it follows that the condition C·δ11=1 must be fulfilled, from which C=1/δ11, where δ11
is the displacement of the point of mass location in the direction of oscillation caused by the
force P=1. Then formula (2) takes the form: