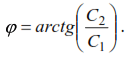Structural Dynamics Concepts

When taking into account the proper mass of the rods of an elastic system, the number of degrees of freedom will be equal to infinity. Fig. 4a shows a beam with a constant along its length by a distributed mass, even in this simplest case, the number of parameters characterizing the position of all points of the beam in a deformed state is equal to infinity. By dividing this beam into sections and replacing the distributed mass with a concentrated mass within each section, we obtain a system with a finite number of degrees of freedom (Fig. 4b).

To better understand the process of oscillations, we will first consider them without taking into account the resistance forces using the example of a weightless simple beam, the mass of which is located in the middle of the span of this beam (Fig. 5). At any moment of time, the displacement of the mass y depends on the elastic force of the beam S (the restoring force) and the inertial force of the moving mass Im . The elastic force tends to return the beam to the equilibrium line and, with any deviations of the mass, will be directed toward the equilibrium line.

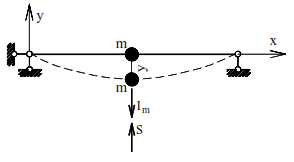
For elastic systems, this force is proportional to the magnitude of the mass deviation from its initial position and can be taken as S=C⋅y, where C is the beam rigidity, determined by the force required to move the point of mass location in the direction of oscillations by one unit; y is the mass deviation from the equilibrium position.
The force of inertia I_m is expressed by the dependence:

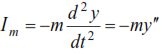
At any given moment in time, the equation of dynamic mass equilibrium has the form:

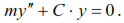
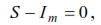
or (1)
Dividing the terms of equality (1) by m and denoting 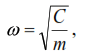(2)

we obtain the equation of free oscillations of a system with one degree of freedom without taking into account the resistance forces:

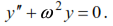
The solution of this homogeneous differential equation is:

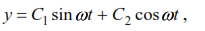
where C1 and C2 are constants of integration determined from the initial conditions:
if t=0, y=y₀ – initial mass deviation;
if t=0, υ=υ₀ – initial mass velocity.
From the first condition C₂ = y₀
From the second condition

At t=0,

Substituting into equation (3) we have:

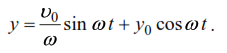
Equation (3) can be reduced to the form:

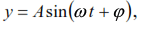
where is the amplitude of oscillations, φ is the initial phase, determined by the expression

Pages: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28