The greater the number of displacements of the system masses, the more complex its calculation. In order to simplify the calculation, the angular displacements of concentrated masses are usually neglected, only their linear displacements are taken into account, and then each mass that has no connections, like a point in a plane, has two degrees of freedom. In addition, very small displacements of masses caused by non-fundamental types of deformations of the system elements for a given type of vibration are neglected. An example
is a weightless elastic rod with a mass m located at its top (Fig. 1). Neglecting the longitudinal deformations of the rod and the vertical displacement of the mass caused by them (transverse vibrations are considered), shear deformations and vertical displacement of the mass during bending of the rod (as small compared to the horizontal displacement from bending of the rod), we obtain a system with one degree of freedom, since the position of the mass is known if the parameter y is known.
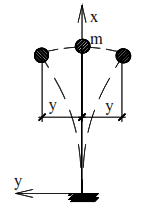
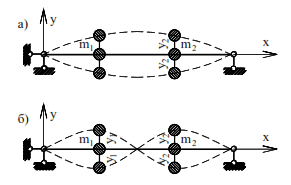
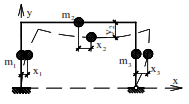
Fig. 2a, b shows a system with two masses and two degrees of freedom, and Fig. 3 shows a system with three masses and four degrees of freedom.