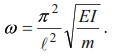Approximate methods and methods of determining frequencies of free oscillations
The calculation of systems with a large number of degrees of freedom by the static method turns out to be very cumbersome and difficult. If in any rod system we take into account the dead weight of at least one of its elements, we obtain a system with an infinite number of degrees of freedom and it is impossible to solve the problem in this formulation without replacing distributed masses by pointed ones using the static method. This fact make engineers to resort to approximate methods.
One of the most common methods of simplifying the solution is to replace the distributed masses of a given system by point masses, i.e., the transition to a system with a finite number of degrees of freedom is made, and the solution can be performed by the static method. By this solution approximate values of frequencies of free oscillations will be obtained. The greater the number of point masses adopted, the more accurate the result obtained, but at the same time the calculation is more complicated. In general, in systems with the number of degrees of freedom equal to infinity, the frequencies of free oscillations are found by approximate methods.
Energy method
This method is based on the law of conservation of energy, according to which at any at any moment of time the sum of potential and kinematic energy of an oscillating system remains constant:
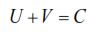
where U,V are the potential and kinetic energies of the system, respectively.
Considering the free oscillations of a system with one degree of freedom, it was found that during the oscillations of the system there is a transition of one type of energy into another. Since Vmin=Umin=0, then from condition (1) it follows that
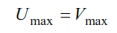
Condition (2) allows us to find the frequency of natural oscillations of the system from the condition of equality of work performed by its forces during oscillations.
The determination of the frequency of natural oscillations by the energy method let us consider the example of a single-span elastic hinged beam of variable stiffness with a distributed mass m(x), which varies according to any law (Fig. 1).
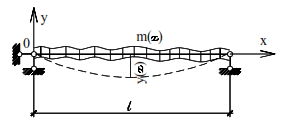
The equation of the curved axis of the beam during oscillation is assumed to be sinusoidal law

where y(x) is the amplitude of oscillation.
For systems whose elements experience primarily bending, neglecting the influence of shear and axial forces, the potential energy is numerically equal to the work of bending moments, i.e.
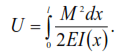
Since ![]() the last equality can be written as
the last equality can be written as
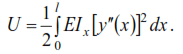
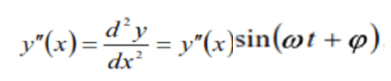
Then equality (4) takes the form
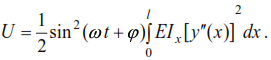
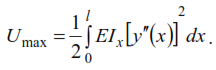
The kinetic energy considering (3) will be:
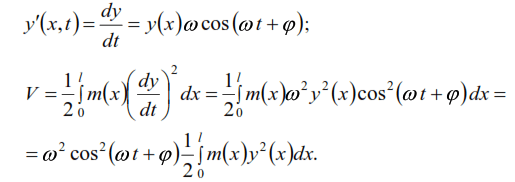
If we assume ![]() ,maximum kinetic energy
,maximum kinetic energy
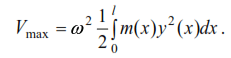
Equating expressions (5) and (6), we find
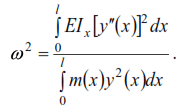
where m is the number of elements of the system.
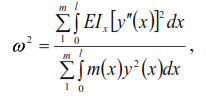
From formula (8) it is clear that the frequencies of natural oscillations of the system can be found by the energy method if the equations of the bent axes of the rods during oscillation are known. The application of the energy method will be traced on the example of an elastic single-span hinged beam of constant cross-section with uniformly distributed mass uniformly distributed throughout the span (Fig. 2).
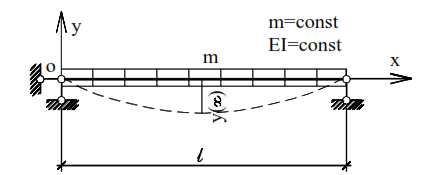
The equation of the curved axis of the beam under oscillations we take the form
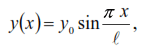
where y0 is the maximum deflection of the beam in the middle of the span from the static equilibrium line (amplitude). It is easy to see that (9) satisfies all the boundary conditions of the considered problem. The frequency of natural vibrations is determined by formula (7). The second derivative of equation (9)
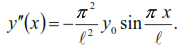
Since EI = const, then the potential energy according to (5)

Kinetic energy according to (6) taking into account (9)
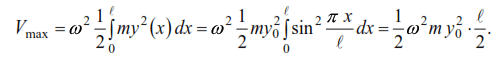
According to formula (7) we have: