Structural Dynamics Concepts

Determination of eigenvectors

According to the concept of eigenvectors, we substitute λ = λ₁ into the first equation of system (32).For the case n = 2 we have:

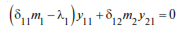
or

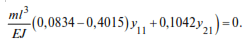
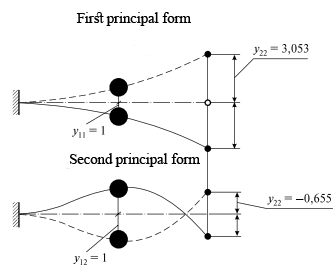
Assuming y₁₁=1, we obtain y₂₁= 3.0528, i.e. the first eigenvector

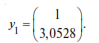
Substituting λ = λ₂ into the same equation, we get:

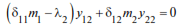
or

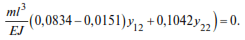
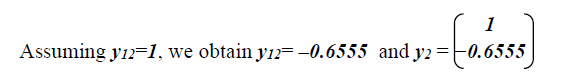
The main oscillation modes corresponding to the found eigenvectors are shown in Fig.

Checking the orthogonality of the main modes of oscillations

To check this, let us use the dependence , which for the case n = 2 looks like this:

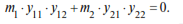
Substituting the found values of the coordinates of the eigenvectors, we obtain:

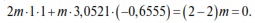
Determination of amplitude forces of inertia in driven oscillations

Let us use the system of equations (40) when n = 2:

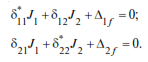
To determine Δ_1f and Δ_2f, the bending moments M_f from the action of the amplitude value of the disturbing force F are plotted (see Fig. 12.2):

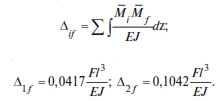
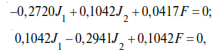
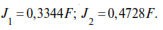
The solution of this problem is supplemented by graphs of the change of inertia forces J₁ and J₂ at different values of θ=αω. Fig. 12.4 shows the above obtained value of inertia forces at θ=0.8ω1.

Pages: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28