Canonical equations for determining the maximum values of inertial forces
Let us consider driven oscillations of an elastic system using the example of a weightless beam with masses subject to dynamic loads (Fig. 12). We will assume that all the disturbing forces acting on the system have the same frequency θ and obey the same law P(t)=Psin(θt), and there are no forces of resistance to the movement of masses. The displacements of masses, the inertial forces of these masses, the forces in the system and its displacements will also be functions of time, obeying the law of load change.
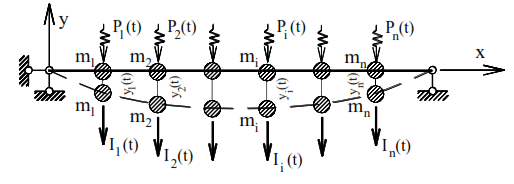
Based on the principle of independence of action of forces, the total displacements of the points of location of masses at any moment in time can be written:
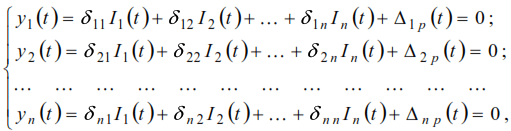
where yi(t) and Ii(t) are, respectively, the displacement of the location point of mass mi and the inertial force of this mass at some point in time t, and Δip(t) is the displacement of mass mi at the same time, caused by the static action of the amplitude value of the dynamic load P(t); δik is the displacement of the i-th mass due to the action of the static force P=1 applied at point k.
The displacement Δip(t) can be written:
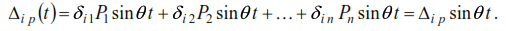
The oscillations of the masses will obey the harmonic law of change of the acting load Psin(θt) and therefore the displacement of the mass mi can be written:
yi(t)=yi·sinθt
(36)
and the second derivative of this equality
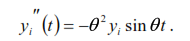
The inertial force is determined by the equality:
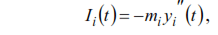
or
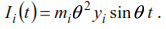
(37)
Taking into account (36),
Then the i-th equation of system (34) will be
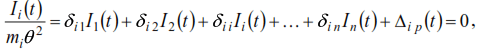
or
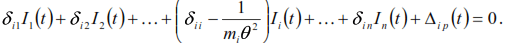
Based on (38) we have:
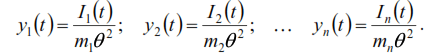
Substituting the expression yi(t) into equation (34) and grouping the terms, we obtain:
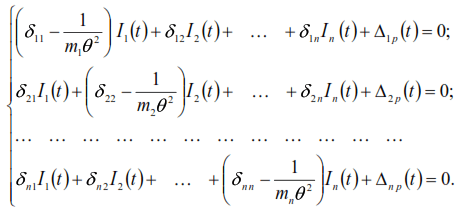
Since all inertial forces in equations (39) are periodic functions Ii(t)=Iisinθt and Δpi(t)=Δpisinθt, then by reducing these equations by sinθt and denoting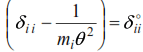 
we obtain:
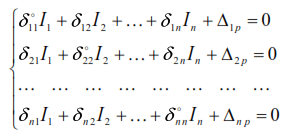
Having solved the system of equations (40), we determine the maximum values of the inertial forces, then calculate the forces and displacements caused by dynamic loads. Systems with many degrees of freedom may be in a state of resonance when the frequency of the disturbing harmonic load coincides with any of the frequencies ω of the natural oscillations of the system. However, the dynamic coefficient, forces and displacements, as a rule, reach their greatest values when the frequency θ coincides with the lowest frequency ω of the natural oscillations of the system. Therefore, in dynamic calculations of structures, the lowest frequency of the natural oscillations of the system is the most important, regardless of whether this system has one or many degrees of freedom. In systems with many degrees of freedom, the lowest frequency of natural oscillations is usually called the fundamental frequency.
