Free oscillations of systems with many degrees of freedom
Let us consider these oscillations using the example of an elastic weightless beam with n point masses without taking into account the resistance forces (Fig. 11). The system under consideration has n degrees of freedom and will have n natural oscillation frequencies ω1, ω2,…. ,ωn , which correspond to the oscillation modes.
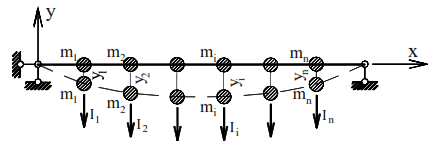
The total displacements of masses under the action of inertial forces I1, I2, …, In can be represented as:
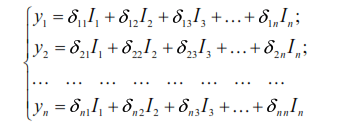
where δii, δik, Ii are respectively the displacements of the points of mass location, by forces P =1 and the inertial forces caused by these masses.
Since the inertial forces Ii= −miyi′′ , then equations (30) can be written
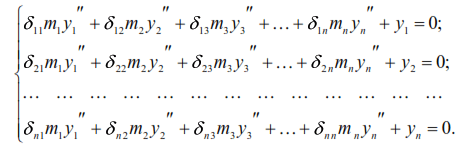
Equations (31) admit the following particular solutions:
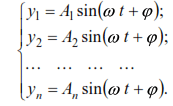
The second derivatives of these solutions are:
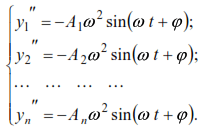
Substituting the expressions y1, y2,… ,yn and their second derivatives into equation (31), reducing by sin(ωt+φ) and grouping the terms, we obtain a system of homogeneous equations in the following form:
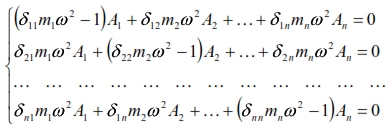
Equations (32) will be valid if we take all the amplitudes A1, A2, …, An equal to zero. But in this case there are no mass movements, the system is at rest on the equilibrium line, and there are no oscillations. If we assume that the amplitudes are different from zero, then such a solution is possible when the determinant of the coefficients at the amplitudes is equal to zero. This is the initial condition for determining the frequencies of the natural oscillations of the system. Dividing all the terms of equations (32) by ω2 and denoting 1/ω2=λ , we obtain the characteristic equation of frequencies, called the secular equation, in the form:
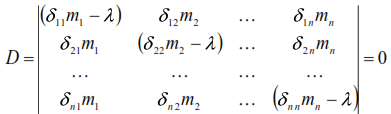
Having expanded equality (33), we obtain an algebraic equation of the n-th degree with respect to λ , and having solved it, we find the value of its roots λ1, λ2,…, λn
According to the formula, we find the oscillation frequencies ω1, ω2,…, ωn.
Equation (33) is valid for any systems (beams, frames, trusses, etc.), both statically determinate and statically indeterminate. In the latter case, the bending moment diagrams (beams, frames) for determining the displacements δii must be constructed from the forces Pi=1 in a given statically indeterminate system, and therefore, when determining the displacements δik, the auxiliary state diagrams 
can be taken in any statically determinate main system of the force method.
In practical calculations, it is usually necessary to know the lowest frequency of natural oscillations ωmin (corresponds to the largest value of the root λmax ), which is usually called the fundamental frequency of oscillations of the system.
The frequencies ω1,ω2,…,ωn, arranged in ascending order, form the frequency spectrum. The principal waveforms are orthogonal to each other. The latter means that the work of external forces, in this case forces of inertia or internal forces caused by them, of any i-th principal form of oscillations on displacements (deformations) caused by another – j-th principal form, is equal to zero.
The orthogonality of the i-th and j-th main forms of oscillations is checked by the formula
where yki,ykj– coordinates yk of the eigenvector corresponding to the i-th and j-th forms of oscillation.
