Example: On the steel I-beam is running engine weight G = 200 kg (Fig. a) creating at N = 2000 rev/min with a vibrational load amplitude value P0 =10kg. Solve four problems of dynamics with the following data: I-beam № 60 with inertia moment I =76806 cm4 and bending resistance moment W =2560 cm3, elastic modulus E = 2∙106 kg/cm2, allowable stress [σ] = 1600 kg/cm2
Solution:
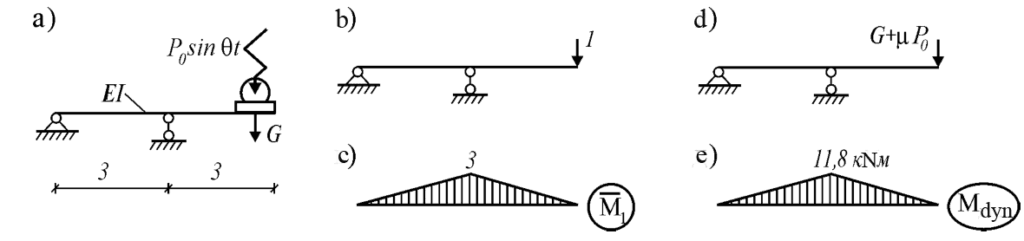
Imagine the initial data in the SI system:
P0=98 N; E=19,6·1010 Н/м2; I=7,68·10-4м4; W=2,56·10-3 м3; [σ]=1,57·108 N/м2
Let’s start with solving the 1st dynamic problem – determining the self frequency.
Calculate it by the formula

yst static deflection will be found by considering
the unite state of (Fig. b), drawing in it a unit diagram M (fig. 2.16 c)
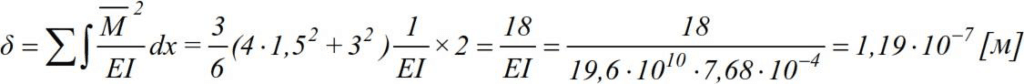

To solve the 2nd problem of dynamics (checking the system for resonance), we calculate the circular engine rotation frequency:
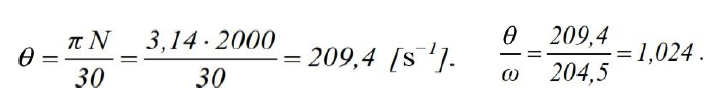
Since 0.7 ≤ θ / ω ≤ 1.3, oscillations occur in resonantly dangerous zone. Therefore, the solution of the problems of dynamics must be continued, and because of the possible occurrence of large amplitudes of oscillations and stresses, they should be calculated taking into account damping.
Solution of the 3rd dynamic problem – we start the system strength test by determining the inelastic resistance coefficient for steel γ=0.01 Then from the formula we define α=γω/2=1.0225, we have μ=20.14 If we do not take into account the damping, we have
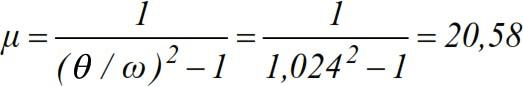
As was to be expected, with low damping (when γ <0.4) and outside the resonantly dangerous zone, accounting for damping has little effect on the magnitude of the dynamic coefficient. At resonance (when θ = ω) taking into account the damping, you would get
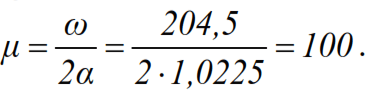
The dynamic moment diagram in the beam will be composed of the sum of the static moment from the engine weight G and the moment from the driven force, reduced to the static force by means of the dynamic coefficient:
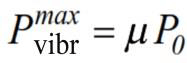
Then we get (Fig. 2.16 e):
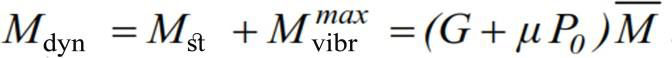
The maximum stress in the beam will be
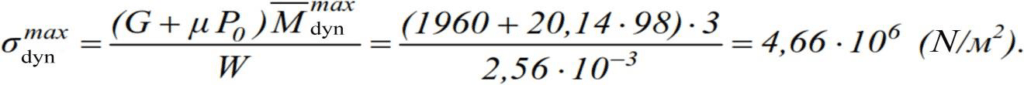
Assuming that this construction will be exploited for a long time, we will take the allowable dynamic stress much less static:

The strength condition of the beam is satisfied:
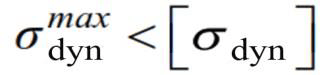
We solve the 4th dynamic problem – we check the system for the allowability of vibration amplitudes. If we assume that the maximum amplitude of oscillations will be at the free end of the cantilever beam, we get
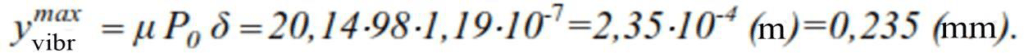
Allowable amplitudes of vibrations acting on a person in eight-hour work shift in a industrial environment
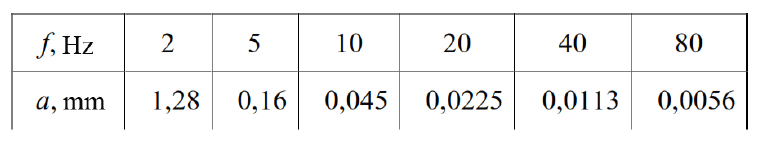
Since the engine frequency f = N / 60 = 2000/60 = 33.3 (Hz), then from table. it follows that the amplitude of oscillations exceeds the permissible.
