Structural Dynamics Concepts

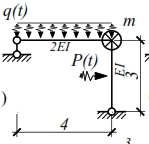
Example: For the given frame, determine the internal forces from the vibration load. Units of measurement: m, kN (not shown in the diagrams). P(t) = 4 sinθt; q(t) = 2 sinθt.

Solution:

1. We perform a kinematic analysis and verify that the system is statically determinate and
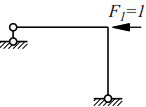
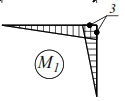
   geometrically unchangeable. Dynamic degree of freedom n=1.
2. We construct a unit diagram M₁ from F₁=1.

3. We determine the displacement:

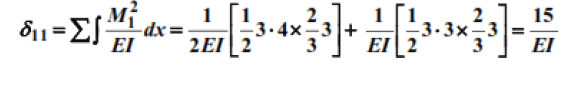
4. Calculate the frequency:

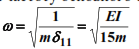
5. We write down the canonical equation for finding the forces of inertia:

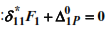
6. We determine the main coefficients of the canonical equation:

at θ=0,8ω:

at θ=1,2ω:

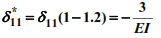
7. We construct the load diagram Мp and determine the free terms of the equation:

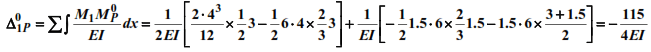
8. We solve the canonical equation and determine the inertial forces:

at θ=0,8ω:

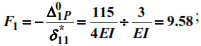
at θ=1,2ω:

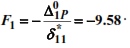
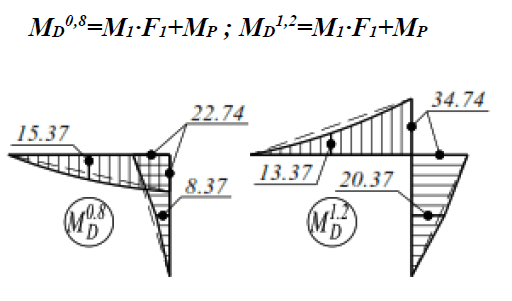
We construct a diagram of dynamic bending moments separately for each frequency.

Pages: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28