Driven oscillations of systems with one degree of freedom
taking into account resistance forces
To obtain a differential equation for this type of oscillation, we will use Figure (9), in which all forces acting on the mass are preserved, and a disturbing load is added, which we will take as harmonic P(t)=Psinθt, coinciding in direction (downward) with the displacement of the mass. Then the equation of dynamic equilibrium will be:
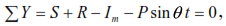
or
Keeping the notation adopted above, we
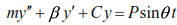
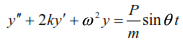
The solution of equation (25) includes the general (18) and particular solution and has the form:

where the first term expresses the free oscillations of the system in the presence of resistance forces, and the second term expresses the forced oscillations, and the first factor of the second term is the oscillation amplitude (ydyn). After the transformations shown above, equation (26) takes the form:
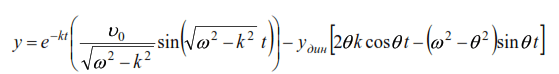
Taking into account the previously adopted notations:

the amplitude of forced oscillations can be represented as
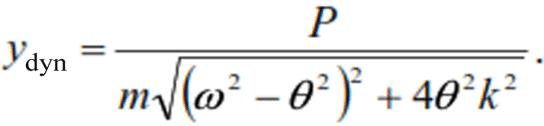
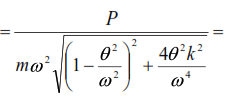
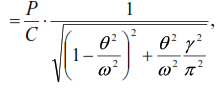
or ydyn=yst·μ;
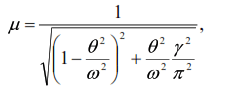
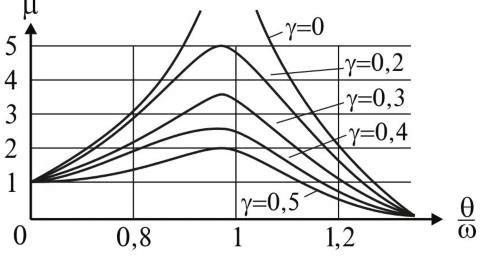
where μ is the dynamic coefficient, the dependence of which on the parameter γ can be
presented in the form of a graph, which is available in educational and reference literature.
From expression (29) it is clear that when the frequencies θ and ω coincide (the case of
resonance), the dynamic coefficient μ does not become infinite (as it does without taking into
account the resistance forces), but has the value μ = π/γ (γ≠0)
For real structures, the absolute value of the decrement γ is significantly less than one. For
example, for metal structures γ = 0.02 − 0.15, for wooden structures – γ = 0.15 − 0.17 etc.
Therefore, in the case of resonance (ω = θ), it is unacceptable that the dynamic coefficient and
the amplitude of oscillations reach
large values, and the structure is at risk of destruction, i.e. even in this case, resonance
remains a great danger for the structure.