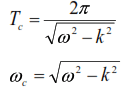Free oscillation of systems with one degree of freedom
taking into account resistance forces
It follows from the graph shown in Fig. 6 that the mass, brought out of the equilibrium state by a dynamic impact, will oscillate with a constant amplitude for an unlimited time. In real conditions, the process of oscillations proceeds differently, since resistance forces are inevitable, preventing oscillations of the mass. This is the resistance of the environment (for example, air), friction in the supporting devices of the system, internal friction of the material particles during the deformation of the system, etc. In the presence of resistance forces, part of the system’s energy is spent (irreversibly) on overcoming these forces and the free oscillations are damped. The influence of resistance forces on an oscillating system is usually taken into account under the assumption that these forces are proportional to the oscillation velocity of the system.
We will trace damped oscillations with accepted initial conditions using the example of an elastic weightless beam with point mass (Fig. 9).
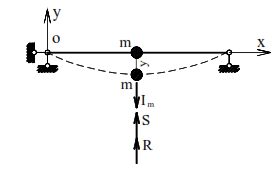
The mass removed from the state of equilibrium is acted upon by the inertial force Im= −my′′,
the elastic force S =Cy and the resistance force R=βy′. The equation of dynamic equilibrium
has the form:
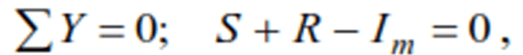
or
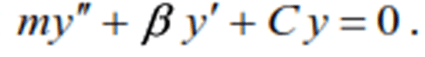
Dividing the terms of the last equality by m, taking into account the relation (2) and denoting
β/m=2k, we obtain:
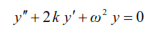
The solution to equation (17) is:
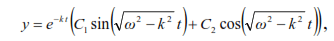
where C1 and C2 are constants of integration that can be found from the initial conditions:
at t=0 y=y0; υ = υ0,
where y0 and υ0 are the initial deviation of the mass from the equilibrium position and its
velocity, respectively.
By the first condition y=C2·1=y0 and C2=y0
By the second condition
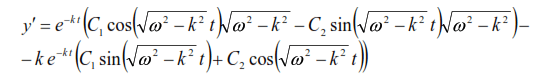
If t=0

and the oscillation equation (6.18) takes the form
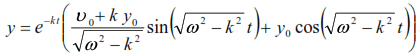
If y0=0 (at t=0 the mass was on the line of static equilibrium), then
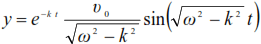
The solution of equation (20) is valid under the condition ω2 > k2
At
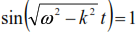
maximum deflection values:
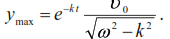
Function (20) has zero ordinates on the t-axis if:
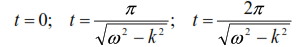
and etc.
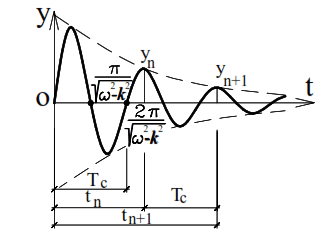
From equation (20) it follows that over time the amplitude of oscillations decreases to zero and the oscillations die out. The graph of such free oscillations is shown in Fig. 10. In this case, the period and circular frequency of free oscillations are determined by the dependencies: