Dynamic deflection can be represented as:
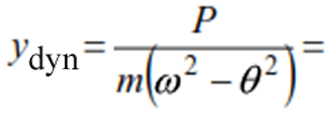
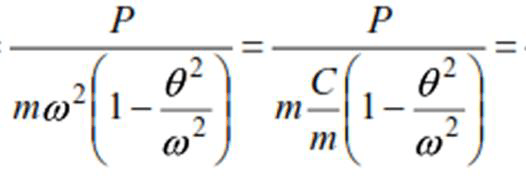
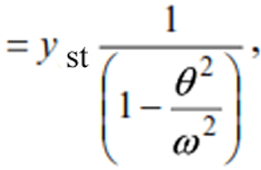
or ydyn=yst·μ ———- ——–(15)
where
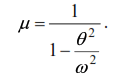
In expression (15), yst is the static deflection, i.e. the deflection caused by the static action of
the amplitude value of the dynamic load P(t).
The abstract quantity μ (16) is called the dynamic coefficient and in systems with one degree
of freedom it expresses the ratio of the dynamic quantities (forces, deflections) to their static
quantities. The graph of the change in the numerical values of the dynamic coefficient is
shown in Fig. 8.
If θ >ω, then the dynamic coefficient μ has negative values and the right curve is located
below the θ/ω axis (shown by the dotted line in Fig. 8). Usually, the values of the coefficient
μ are taken by absolute value and both curves on the graph are located above the θ/ω axis
(Fig. 8).
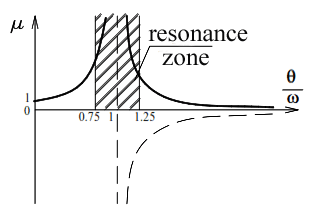
From formula (16) it is evident that as the frequency of the disturbing force θ approaches the frequency of free oscillations ω, the dynamic coefficient, as well as the dynamic deflection (15), rapidly increase. When the frequencies are equal (ω=θ), the dynamic coefficient becomes equal to infinity.
This case in construction is called the resonance phenomenon and is a great danger for the structure, since the forces, displacements and stresses in the elements of the system reach high values. For important structures, not only resonance phenomena are unacceptable, but also conditions under which these structures would be in the resonance zone (Fig. 8). To avoid resonance, a condition is usually ensured that the frequency of free oscillations of the system differs from the frequency of its driven oscillations by 25-30%.
